Cours Econométrie
Les différentes parties du cours
Introduction
- Présentation est disponible!
- Résumé
- Modèle économétrique : établit une relation, plus ou moins approximative, permettant d'expliquer une variable d'intérêt y en fonction d'autres variables x(1), ⋯, x(p), qui se traduit mathématiquement : y ≃ f(x(1), ⋯, x(p))
- Notion de causalité : cette relation n'est pas symmétrique puisque les variables x(1), ⋯, x(p), dites explicatives, sont supposées être les causes des variations de la variable y, dite à expliquer.
- Nature approximative de la relation : se traduit en économétrie par l'ajout d'un bruit U de nature aléatoire
Y = f(x(1), ⋯, x(p))+U
rendant la nature de la variable d'intérêt aléatoire et ainsi notée Y (convention: majuscule désigne une variable aléatoire). - Tendance (déterministe) et bruit (aléatoire) : la tendance correspond à la partie informative dans la relation quand le bruit (non-informatif) n'est qu'une perturbation de la tendance.
- en moyenne, les valeurs de U se compensent : $\Bbb{E}(U)=0$ (i.e. le bruit est d'espérance mathématique nulle).
- le niveau du bruit est mesuré par son écart-type $\sigma_U=\sigma(U)=\sqrt{\Bbb{V}ar(U)}$ (ou par sa variance $\sigma_U^2=\Bbb{V}ar(U)$) est tout naturellement considéré comme un paramètre de nuisance.
- Linéarité de la tendance : dans un cours d'introduction à l'économétrie, la relation f entre la variable à expliquer et les variables explicatives est supposée linéaire :
Y = β0 + β1 × x(1) + ⋯ + βp × x(p) + U - Gaussianité du bruit : il est parfois supposé que U ⤳ N(0, σU)
- Relation avec cours de statistique descriptive (L1) : il est facile d'obtenir une représentation graphique lorsqu'on ne considère qu'une seule (p = 1) variable explicative x = x(1) (aussi appelée régresseur):
Y = β0 + β1 × x + U - Relation avec cours de statistique inférentielle (L2) : le cas (très particulier) p = 0 où aucune variable explicative est envisagée, correspond au cadre d'un cours de statistique inférentielle (de L2). Mathématiquement, on a :
$$Y=\beta_0 + U \Longleftrightarrow \mu:=\Bbb{E}(Y)=\beta_0\mbox{ et }\sigma^2:=\Bbb{V}ar(Y)=\sigma^2_U $$
Dans le cadre Gaussien, on écrit :
Y ⤳ N(μ, σ)⇔Y ⤳ N(β0, σU)
N.B. : ce commentaire nous informe que la plupart des outils de statistique inférentielle (intervalle de confiance et test d'hypothèses) seront utilisés dans ce cours de L3. - Définition de modèle : sous-entend que plusieurs individus (statistiques) sont gérés par l'unique équation définissant le modèle. Mathématiquement, chaque individu est alors caractérisé par un indice, noté i (dans le cas général) et t (pour représenter un temps) :
Yi = β0 + β1 × xi(1) + ⋯ + βp × xi(p) + Ui
Les membres de l'équation ne laissant pas apparâitre l'indice i sont les paramètres du modèle. Il y en a p + 2 : les p + 1 paramètres βj, parfois dits de régression, mais aussi σU = σ(Ui) le paramètre de nuisance. - Jeu de données : en économétrie (comme en statistique), nous disposerons de n données représentées sous la forme :
$$ \left\{\begin{array}{llc} y_1&=&\beta_0+\beta_1\times x_1^{(1)}+\cdots+\beta_p\times x_1^{(p)}+u_1\\ \vdots & \vdots& \vdots\\ y_i&=&\beta_0+\beta_1\times x_i^{(1)}+\cdots+\beta_p\times x_i^{(p)}+u_i\\ \vdots & \vdots& \vdots\\ y_n&=&\beta_0+\beta_1\times x_n^{(1)}+\cdots+\beta_p\times x_n^{(p)}+u_n\\ \end{array}\right. $$
Matriciellement, le système s'écrit de manière très synthétique :
$$ \mathbf{y} = \underline{\mathbf{x}}\mathbf{\beta} + \mathbf{u} $$
où
$$ \mathbf{y}=\left(\begin{array}{c}y_1\\\vdots\\ y_i\\\vdots\\ y_n\end{array}\right), \underline{\mathbf{x}}=\left(\begin{array}{cccc}1 & x_1^{(1)} &\cdots & x_1^{(p)} \\\vdots & \vdots & & \vdots\\ 1 & x_i^{(1)} &\cdots & x_i^{(p)}\\\vdots& \vdots & & \vdots\\ 1 & x_n^{(1)} &\cdots & x_n^{(p)}\end{array}\right), \mathbf{u}=\left(\begin{array}{c}u_1\\\vdots\\ u_i\\\vdots\\ u_n\end{array}\right) \mbox{ et } \mathbf{\beta}=\left(\begin{array}{c}\beta_0\\\vdots\\ \beta_j\\\vdots\\ \beta_p\end{array}\right) $$ - Comprendre (expérimentalement) le modèle : Un expérimentateur se propose de mieux comprendre le modèle Yi = β0 + β1 × xi + Ui (avec U ⤳ N(0, σU)) en génèrant un jeu de n = 10 données après avoir fixé les valeurs de β0, β1 et σU qui restent inconnues de nous comme c'est le cas dans une étude réelle.
- un point bleu i a pour coordonnées (xi, yi).
- la droite rouge représente le modèle inconnu.
- les flêches rouges représentent les ui inconnus, les sens des flèches indiquant les signes de leurs valeurs..
- le code des couleurs est clair : "bleu" signifie connu (ou donné ou observé) quand "rouge" signifie inconnu.
- les traits en pointillé noir indique la direction naturelle dans lequelle l'équation a du sens (i.e. selon l'axe des ordonnées y).
- un yi est obtenu à partir de xi :
- en partant du point de coordonnées (xi, 0) sur l'axe des abscisses
- puis en montant verticalement le long du trait en pointillé noir jusqu'à la droite rouge pour arriver au point de coordonnées (xi, β0 + β1 × xi)
- et finalement d'ajouter la perturbation du bruit ui pour arriver au point bleu de coordonnées (xi, yi)=(xi, β0 + β1 × xi + ui).
- Comprendre l'enjeu de faire l'hypothèse du modèle linéaire : une personne avisée (atteignant donc un certain niveau d'expertise en économétrie) comprend que faire l'hypothèse d'un modèle linéaire consiste à accepter que le jeu de données étudié est issu de ce modèle linéaire, à savoir que le processus d'obtention des données est (approximativement) le même que le procédé de construction décrit au point précédent.
- Estimer le modèle :
- Le modèle (ou plutôt sa tendance) est représenté(e) par la droite rouge, caractérisé(e) par les paramètres β0 (son ordonnée à l'origine) et β1 (sa pente) qui sont donc inconnus. Malgré cela, le jeu de données est connu puisqu'observé (même s'il est supposé dériver de la droite rouge inconnu), ici fourni par l'expérimentateur (les points bleus).
- En utilisant la propriété de la droite rouge de passer en "plein milieu" du nuage de points bleus (en théorie, d'un nuage constitué d'une inifinité de points bleus), une méthode d'estimation de la droite rouge inconnue est de déterminer l'unique droite bleue la plus proche (dans la direction verticale, i.e. le long des traits en pointillé noir) de tous les points bleus. Un petit souvenir du cours de statistique descriptive de L1 nous conduit aux pente et ordonnée à l'origine de cette droite bleue :
$$\widehat{\beta_1}=cov(y,x)/var(x) \mbox{ et }\widehat{\beta_0}=\overline{y} - \widehat{\beta_1}\times \overline{x}$$
- Résidus : la dernière étape consiste à déterminer les "remplaçants" $\widehat{u_i}$ des bruits ui, appelés résidus et représentés par les flêches rouges. Puisque ces flêches rouges sont les écarts (verticaux) des points bleus à la droite rouge, il est naturel de définir leurs "remplaçants" par les écarts (verticaux) des points bleus à la droite (estimée) bleue :
- En conclusion, dans ce dernier exemple expérimental, nous avons abordé la plupart des ingrédients qui nous seront utiles pour comprendre les estimations dans le cadre général où le nombre p de variables explicatives n'est pas limité à 1.
- FAQ (Foire Aux Questions) :
Q : Pourquoi avoir insisté sur le processus de construction du jeu de données ?
R : Dans la réalité, il y a trop de praticiens qui appliquent de manière automatique la méthode d'estimation (par moindres carrés) sans remettre en cause l'hypothèse faite sur le modèle linéaire. Le processus de construction permet de décomposer les différentes étapes d'obtention des réalisations yi des Yi à partir des xi. L'objectif est de faire réaliser à l'utilisateur que ses données sont alors supposées avoir été obtenues par un tel procédé de construction. Dans le cas de régression simple, i.e. p = 1, on peut toujours se reposer sur une représentation graphique. Il en est éventuellement de même lorsque p = 2 avec une représentation graphique du nuage de points en dimension 3. En dimension supérieure, cela est quasiment impossible et on doit bien réaliser que tous les résultats d'estimation obtenus ne sont valides que si le modèle linéaire est le vrai modèle (à une légère approximation près).
- Testez-vous!
q1. Dans les graphes ci-dessus que représente un élément graphique en bleu ?
q2. Dans les graphes ci-dessus que représente un élément graphique en rouge ?
q3. Comment nomme-t'on $\widehat{u}_i$ associé à la iême donnée?
q3. Comment nomme-t'on $\widehat{y}_i$ associé à la iême donnée?
Les estimations par la méthode des Moindres Carrés (Ordinaire)
- Présentation est disponible!
- Résumé
- Objectif : estimer à partir des données (i.e. le nuage de points) {(yi,xi)}i = {(yi,xi(1),⋯,xi(p))}i, les paramètres inconnus βj. Sous l'hypothèse du modèle linéaire, on a :
$$ \mathbf{y} = \underline{\mathbf{x}}\mathbf{\beta} + \mathbf{u} $$ - Espace (de représentation) des individus Dans le cas p = 1, on a les données représentées sous forme d'un nuage de points bleus :
- Notre objectif est de chercher la droite bleue la plus proche du nuage de points bleus dont voilà la solution :
- Lorsque p = 2, la solution est ici de déterminer un plan bleu le plus proche du nuage de points :
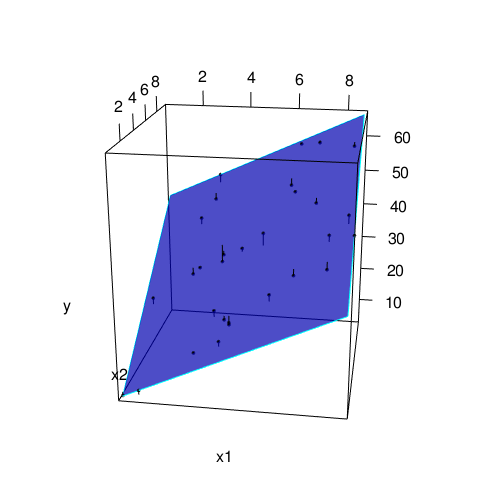
- Méthode des Moindres Carrés (Ordinaire) : trouver les $\widehat{\mathbf{\beta}}$ de sorte que pour tout $\mathbf{\alpha}\neq \widehat{\mathbf{\beta}}$:
$$\||\mathbf{y}-\underline{\mathbf{x}}\widehat{\mathbf{\beta}}\||^2 < \||\mathbf{y}-\underline{\mathbf{x}}\mathbf{\alpha} \||^2$$
avec
$$\||\mathbf{y}-\underline{\mathbf{x}}\mathbf{\alpha} \||^2=\sum_{i=1}^n \left(y_i - (\alpha_0+\alpha_1 x^{(1)}_i+\cdots+\alpha_p x^{(p)}_i) \right)^2$$
représentant la somme des carrés des écarts des points à un plan (une droite pour p = 1) ayant pour coefficients α = (α0, α1, ⋯, αp) La solution d'un tel problème se résout plus facilement dans l'espace des variables en cherchant le vecteur $\widehat{\mathbf{y}}=\underline{\mathbf{x}}\widehat{\mathbf{\beta}}$ le plus proche du vecteur y.
- Espace (de représentation) des variables : pour p = 2 (raisonnement restant valable pour p quelconque) et en posant x0 = 1, on a la représentation suivante :
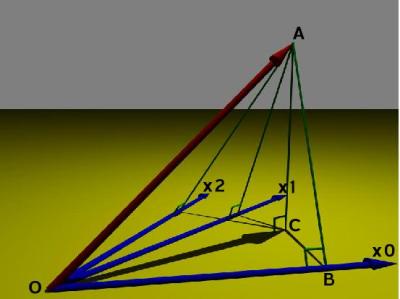
$$\mathbf{\widehat{y}}=\widehat{\beta_0} \mathbf{1} + \widehat{\beta_1} \mathbf{x_1} + \widehat{\beta_2} \mathbf{x_2} = \underline{\mathbf{x}} \widehat{\mathbf{\beta}} $$
En s'appuyant sur les mathématiques, comme $\widehat{\mathbf{y}}$ est le projeté (orthogonalement) de y sur le plan jaune, on a :
$$\widehat{\mathbf{y}}=\underbrace{\underline{\mathbf{x}}(\underline{\mathbf{x}}^T\underline{\mathbf{x}})^{-1}\underline{\mathbf{x}}^T}_{\text{operateur de projection}}\mathbf{y}$$
et donc
$$\widehat{\mathbf{y}}=\underline{\mathbf{x}}\underbrace{(\underline{\mathbf{x}}^T\underline{\mathbf{x}})^{-1}\underline{\mathbf{x}}^T\mathbf{y}}_{\widehat{\mathbf{\beta}}}$$
Ainsi, l'estimateur par la méthode des Moindres Carrés (Ordinaire) est :
$$\widehat{\mathbf{\beta}}=(\underline{\mathbf{x}}^T\underline{\mathbf{x}})^{-1}\underline{\mathbf{x}}^T\mathbf{y}$$ - Dans le cas p = 1,
- $\widehat{\beta_1}(\mathbf{Y}|\mathbf{x^{(1)}})=cov(\mathbf{Y},\mathbf{x^{(1)}})/var(\mathbf{x^{(1)}})$
- $\widehat{\beta_0}(\mathbf{Y}|\mathbf{x^{(1)}})=\overline{Y} - \widehat{\beta_1}(\mathbf{Y}|\mathbf{x^{(1)}})\times \overline{x^{(1)}}$
- Les résidus $\widehat{\mathbf{u}}$ : les écarts des points au plan (ou droite) bleu(e) s'obtiennent par $\widehat{\mathbf{u}}=\mathbf{y}-\underbrace{\underline{\mathbf{x}}\widehat{\mathbf{\beta}} }_{\widehat{\mathbf{y}}}$
- Estimation du niveau de bruit $\sigma_U=\sqrt{\mathbb{E}(U_i^2)}$ :
$$ \widehat{\sigma_U}(\mathbf{y}|\underline{\mathbf{x}})=\sqrt{\frac 1{n-p-1}\sum_{i=1}^n \widehat{u_i}^2} $$ - Qualité d'ajustement linéaire

La qualité d'estimation sera d'autant meilleure que le vecteur $\widehat{\mathbf{y}}$ (i.e. $\overrightarrow{OC}$) est ressemblant à y (i.e. $\overrightarrow{OA}$). Le carré du cosinus (coefficient de détermination) de l'angle entre y et $\widehat{\mathbf{y}}$ est alors d'autant plus proche de 1.
$$R^2=cos^2(\widehat{AOC})=\frac{\|\widehat{\mathbf{y}}-\overline{\mathbf{y}}\|^2}{\|\mathbf{y}-\overline{\mathbf{y}}\|^2}=\frac{var(\widehat{\mathbf{y}})}{var(\mathbf{y})}=\text{part de variance expliquée par le modèle}$$ Qualité d'estimation : De part la nature aléatoire du bruit Ui , il en résulte que les estimations $\widehat{\beta_j}(\mathbf{Y}|\underline{\mathbf{x}})$ sont différentes selon le nuage de points réalisés. En pratique, on observe un unique jeu de données $(\mathbf{y},\underline{\mathbf{x}})$ qui est un parmi une infinité de nuages de points $(\mathbf{y_{[k]}},\underline{\mathbf{x}})$ (k = 1⋯, + ∞). On obtient alors une unique estimation $\widehat{\beta_j}(\mathbf{y}|\underline{\mathbf{x}})$ qui est une parmi une infinité des estimations de βj que l'on aurait pu avoir $\widehat{\beta_j} \left(\mathbf{ y}_{[k]} | \underline{ \mathbf{x}} \right)$ (k = 1, ⋯, +∞) C'est impossible mais si vous disposiez de l'infinité des estimations $\widehat{\beta_j} \left(\mathbf{ y}_{[k]} | \underline{ \mathbf{x}} \right)$ (k = 1, ⋯, +∞), comment mesureriez-vous la qualité d'estimation de βj ? La solution est l'écart-type $\sigma_{\widehat{\beta_j}}$ de toutes les estimations :
$$ \overleftrightarrow{\left(\widehat{\beta_j} \left(\mathbf{ y}_{[\cdot]} | \underline{ \mathbf{x}} \right)\right)}_{+\infty}=\lim_{m\to +\infty} \sqrt{\frac1m\sum_{k=1}^m \left(\widehat{\beta_j} \left(\mathbf{ y}_{[k]} | \underline{ \mathbf{x}} \right) - \overline{\left(\widehat{\beta_j} \left(\mathbf{ y}_{[\cdot]} | \underline{ \mathbf{x}} \right)\right)}_{+\infty} \right)^2} $$Estimation de la qualité d'estimation : Puisque $\sigma_{\widehat{\beta_j}}$ est inconnu, il faut l'estimer. Mathématiquement, on a la formule suivante :
$$ \sigma_{\widehat{\beta_j}}=\sigma_U \times \sqrt{\left(\left(\mathbf{\underline{x}}^T\mathbf{\underline{x}}\right)^{-1}\right)_{j+1,j+1}} $$
On constate que la seule inconnue est donc σU que l'on sait estimer.
Erreur standard : estimation $\widehat{\sigma_{\widehat{\beta_j}}}(\mathbf{y}|\underline{\mathbf{x}})$ de la qualité d'estimation $\sigma_{\widehat{\beta_j}}$ de βj s'obtient par :
$$ \widehat{\sigma_{\widehat{\beta_j}}}(\mathbf{y}|\underline{\mathbf{x}})=\widehat{\sigma_U}(\mathbf{y}|\underline{\mathbf{x}})\times \sqrt{\left(\left(\mathbf{\underline{x}}^T\mathbf{\underline{x}}\right)^{-1}\right)_{j+1,j+1}} $$ - Objectif : estimer à partir des données (i.e. le nuage de points) {(yi,xi)}i = {(yi,xi(1),⋯,xi(p))}i, les paramètres inconnus βj. Sous l'hypothèse du modèle linéaire, on a :
- Quelques Travaux Pratiques (pour ceux qui sont motivés, c-à-d tout le monde, et qui ont accès à un ordinateur, en cours ou à la maison) :
- Après avoir installé R et RStudio
- Créer un répertoire de travail (en évitant les espaces dans les chemins)
- Télécharger les données R (dans le répertoire de travail) : cinema dataLM
- Dans RStudio (Menu
Session), fixer le répertoire de travail (set working directory) au répertoire nouvellement créé - Pour l'exercice 1 de la fiche de TD 1 :
attach("cinema.RData")attach(cinema)head(cinema)pour découvrir le début des variables du jeu de donnéescinemamean(log(freq))etvar(log(freq))pour obtenir les moyenne et variance de la variablelog(freq)- tout est en place pour faire l'exercice 1 ...
- Pour l'exercice 2, le jeu de données
canadase trouve dansdataLM.RData:attach("dataLM.RData")attach(canada)
- Pour info : après chaque exo, il est bon d'éxecuter autant de fois l'instruction
detach()que vous avez fait desattach(), i.e. 2 fois pour les 2 premiers exercices de la fiche de TD 1.
FAQ (A compléter en fonction des questions posées en cours)
Les tests de significativité
- Rappel cours de L2 (en reconstruction) ou via AEP
- Exo 1 : On souhaite dans cet exercice vérifier les hypothèses de Keynes à partir d'un jeu de données :
- la propension marginale à consommer est-elle inférieure à 1 ? On pourra répondre aux questions suivantes :
- comment se décrit l'affirmation d'intérêt en fonction du paramètre d'intérêt β1 ? en fonction du paramètre d'écart $\delta_{\beta_1,1}:=\frac{\beta_1-1}{\sigma_{\widehat{\beta_1}}}$ ?
Réponse
H1 : β1 < 1 équivalent à H1 : δβ1, 1 < 0
- quelle est la pire des (mauvaises) situations pour décider l'affirmation d'intérêt au vu des données ?
Réponse
H0 : β1 = 1
- quel est le comportement aléatoire de $\widehat{\delta}_{\beta_1,1}(\mathbf{Y}|\underline{\mathbf{x}})$ dans la pire des situations ?
Réponse
Sous H0, $\widehat{\delta}_{\beta_1,1}(\mathbf{Y}|\underline{\mathbf{x}})=\frac{\widehat{\beta_1}(\mathbf{Y}|\underline{\mathbf{x}})-1}{\widehat{\sigma}_{\widehat\beta_1}(\mathbf{Y}|\underline{\mathbf{x}})}\stackrel{approx.}{\leadsto} \mathcal{N}(0,1)$.
- pourquoi se place-t'on dans la pire des situations pour construire la règle de décision ?
Réponse
Parce dans cette situation H0, appelée la pire des mauvaises situations (non H1), le risque de décider l'affirmation d'intérêt (H1) à tort avec les données est maximal.
- peut-on construire la règle de décision à un seuil α en raisonnant sur le paramètre d'intérêt ? sur le paramètre d'écart ?
Réponse
Uniquement à partir du paramètre d'écart δβ1, 1 car à partir du paramètre d'intérêt β1 on ne pourrait connaître la loi de probabilité de son estimateur $\widehat\beta_1(\mathbf{Y}|\underline{\mathbf{x}})$ même sous H0
- si vous avez répondu oui à l'une des deux questions précédentes (ce que nous espérons), calculez le quantile associé à la règle de décision pour un seuil de signification de 5% ?
Réponse
Sous la loi 𝒩(0, 1) représentant l'ensemble de toutes les estimations possibles de $\widehat{\delta}_{\beta_1,1}(\mathbf{Y}|\underline{\mathbf{x}})$ sous H0, on veut écarter 5% (les plus à gauche) qui nous conduiraient de dire à tort que l'affirmation d'intérêt est vraie. Cela revient à choisir $\delta_{lim,5\%}^-\stackrel{R}{=}qnorm(.05)=-qnorm(.95)=-1.644854$ La Règle de Décision s'exprime donc : accepter H1 si $\widehat{\delta}_{\beta_1,1}(\mathbf{y}|\underline{\mathbf{x}})<\delta_{lim,5\%}^-$
- nous sommes le jour J, quelles sont les estimations des paramètres et en particulier les valeurs de $\widehat{\beta}_1(\mathbf{y}|\underline{\mathbf{x}})$ et $\widehat{\delta}_{\beta_1,1}(\mathbf{y}|\underline{\mathbf{x}})$ ? Appliquez alors la règle de décision (voir indication ci-dessous).
Réponse
En conclusion, puisque $\widehat{\beta}_1(\mathbf{y}|\underline{\mathbf{x}})=0.6654$ et $\widehat{\delta}_{\beta_1,1}(\mathbf{y}|\underline{\mathbf{x}})=-90.4$
- quelle est la règle de décision alternative basée sur l'indicateur du niveau de fiabilité de la règle de décision ?
Réponse
A α = 5%, nous avons accepté l'affirmation d'intérêt H1 avec notre jeu de données. On peut ensuite s'intéresser au plus petit risque α à encourir au vu des données pour accepter H1. En fait, ce risque, appelé p-valeur (p-value en anglais) est d'une certaine manière le risque d'intérêt associé l'affirmation d'intérêt. En effet, on peut reformuler la Règle de Décision encore plus intuitivement de la manière équivalente suivante :
Accepter H1 si p-valeur < α (littéralement : le risque pour accepter H1 est raisonnablement faible). - rédigez le test sous une forme standard.
Réponse
Rassemblons tous les éléments même techniques sous un format assez standard :
Hypothèses de test : H0 : β1 = 1 contre H1 : β1 < 1
Statistique de test sous H0 : $\widehat{\delta}_{\beta_1,1}(\mathbf{Y}|\underline{\mathbf{x}})=\frac{\widehat{\beta_1}(\mathbf{Y}|\underline{\mathbf{x}})-1}{\widehat{\sigma}_{\widehat\beta_1}(\mathbf{Y}|\underline{\mathbf{x}})}\stackrel{approx.}{\leadsto} \mathcal{N}(0,1)$
Règle de Décision : Accepter H1 si p − valeur < α (ou $\widehat{\delta}_{\beta_1,1}(\mathbf{y}|\underline{\mathbf{x}})<\delta_{lim,\alpha}^-$)
Conclusion : Puisqu'au vu des données,
$p-valeur (gauche)\stackrel{R}{=}pnorm((0.6654-1)/0.003702)=0<5\%$
on peut plutôt penser que la propension marginale à consommer est strictement inférieure à 1.$
- comment se décrit l'affirmation d'intérêt en fonction du paramètre d'intérêt β1 ? en fonction du paramètre d'écart $\delta_{\beta_1,1}:=\frac{\beta_1-1}{\sigma_{\widehat{\beta_1}}}$ ?
- La propension marginale à consommer est-elle strictement positive au seuil de 5% ?
Réponse
En complément de la rédaction standard, il est plus intéressant de proposer une rédaction abrégée qui n'extrait que l'essentiel sur un plan pratique (sans se soucier des aspects techniques).
Rédaction abrégée
Affirmation d'intérêt : H1 : β1 > 0
Conclusion : Puisqu'au vu des données, $p-valeur (droite)\stackrel{R}{=}1-pnorm((0.6654-0)/0.003702)=1-pnorm(179.7)=0<5\%$
on peut plutôt penser que la propension marginale à consommer est strictement positive.
Rmq : la p-valeur précédente n'était pas fournie directement dans l'énoncé. Pour obtenir sa valeur, il faut s'appuyer sur les relations entre p-valeurs (ici) droite et bilatérale. En effet, la p-valeur bilatérale correspond ici à celle relative au test de significativité locale associé à H1 : β1 ≠ 0 et fourni dans lesummary(lm(CONSO~REVENU)). Comme la p-valeur droite est (ici) 2 fois plus petite que la p-valeur bilatérale qui vaut 0 (dernière colonne de la partie "coefficients"), on en déduit sa valeur 0/2 = 0. - Sans calcul suppléméntaire montrez que la propension marginale est différente de zéro au seuil de 5%. Ce test porte le nom plus connu de test de significativité locale car il permet de montrer que le régresseur REVENU apporte une information significative dans l'explication de la variable à expliquer CONSO.
Réponse
La réponse est directement à lire en 4ème ou dernière colonne de la partie "coefficients" du
summary(lm(CONSO~REVENU))ci-dessous. Rmq : si on n'avait pas proposé en indication la sortie dusummary(lm(CONSO~REVENU))mais uniquement l'instruction Rpnorm((0.6654-0)/0.003702)(ce qui peut être le cas en examen), il aurait fallu pour déduire la p-valeur du test de significativité locale faire en R2*(1-pnorm((0.6654-0)/0.003702)). - La consommation incompressible est-elle strictement positive (toujours au seuil de 5%) ?
- Un néophyte a souhaité effectuer un test au seuil de 5% pour essayer de savoir si β1 > 0.7 et a obtenu avec ses données et son logiciel préféré une p-valeur de l'ordre de 99.2%.
- Proposez l'instruction R qui permet d'obtenir la valeur de cette p−valeur.
- Comment doit-il conclure au test qu'il a mis en place ?
- Peut-il conclure autre chose ?
- Quel est le risque mimimum qu'il doit prendre s'il souhaite montrer que β1 ≠ 0.7 ?
Indication: (Pour jouer avec R, éxecuter : attach("dataLM.RData");attach(canada))
R> summary(lm(CONSO~REVENU)) Call: lm(formula = CONSO ~ REVENU) Residuals: Min 1Q Median 3Q Max -14477.4 -1322.4 713.9 2168.2 11107.3 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.723e+03 1.280e+03 2.909 0.00645 ** REVENU 6.654e-01 3.702e-03 179.744 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 4773 on 33 degrees of freedom Multiple R-squared: 0.999, Adjusted R-squared: 0.9989 F-statistic: 3.231e+04 on 1 and 33 DF, p-value: < 2.2e-16 R> (0.6654-1)/0.003702 [1] -90.38358 R> pt(-90.38358,35-2) [1] 2.06455e-41 R> pnorm(-90.38358) [1] 0
- Exo 2 (consommation de champage) : On souhaite étudier l'influence du revenu personnel (variable
R), du prix du champagne (variableP)et du prix des liqueurs (variablePL) sur la consommation de champagne (variableC). Un spécialiste pense qu'un modèle adapté est le modèle log-linéaire suivant :
log(Ci)=β0 + β1log(Ri)+β2log(Pi)+β3log(PLi)+Ui
On supposera que le bruit Ui est centré et de variance σU2.
- Ce modèle est-il très loin du modèle linéaire (traité depuis le début de l'année) ?
- Quelles sont les estimations des paramètres basés sur le jeu de données
champ? - Complétez : lorsque le revenu
_ _ _ _ _ _ _de 10%, la consommation de champagne_ _ _ _ _ _ _approximativement de_ _ _ _ _ _ _. - Peut-on penser que le régresseur prix du champagne (
P) apporte de l'information dans l'explication de la consommation de champagne, i.e. est-il significatif ? (Indication : conditions mathématiques d'utilisation à préciser si nécessaire) - Même question pour le régresseur revenu (
R). - Même question pour le régresseur prix des liqueurs (
PL). - Peut-on penser au seuil de 5% que le champagne est un produit de luxe ?
Indication: (Pour jouer avec R, éxecuter : attach("dataLM.RData") SAUF si déjà fait avant!)
R> champ C R P PL 1 42.5 57.2 76.60 73.6 2 38.7 59.1 80.70 72.9 3 40.0 61.5 86.80 67.0 4 45.4 64.0 85.40 63.2 5 51.7 67.6 84.10 55.1 6 65.4 71.7 81.70 59.2 7 72.4 75.5 80.90 65.6 8 59.0 76.2 91.70 59.5 9 61.3 78.0 96.50 56.8 10 75.6 81.9 95.40 61.3 11 82.5 86.6 96.20 73.0 12 90.5 93.0 98.41 88.9 13 100.0 100.0 100.00 100.0 14 110.5 105.4 99.30 111.4 15 127.9 109.8 97.80 123.3 16 139.0 115.0 96.00 136.9 17 143.8 120.5 104.30 150.6 R> summary(lm(log(C)~log(R)+log(P)+log(PL),data=champ)) Call: lm(formula = log(C) ~ log(R) + log(P) + log(PL), data = champ) Residuals: Min 1Q Median 3Q Max -0.066608 -0.031357 -0.006315 0.022400 0.067713 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.48769 0.74597 0.654 0.5247 log(R) 2.36686 0.13037 18.155 1.28e-10 *** log(P) -1.36409 0.24213 -5.634 8.15e-05 *** log(PL) -0.10679 0.06013 -1.776 0.0991 . --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.04215 on 13 degrees of freedom Multiple R-squared: 0.9923, Adjusted R-squared: 0.9906 F-statistic: 560.5 on 3 and 13 DF, p-value: 5.408e-14 R> qt(.975,17-3-1) [1] 2.160369 R> qnorm(.975) [1] 1.959964 R> #################### R> 1-pt( (2.36686-1)/0.13037,13 ) [1] 5.181925e-08
- FAQ (A compléter en fonction des questions posées en cours)
Phénomène de colinéarité
- Résumé de cours
- Prérequis pour jouer avec
R- Télécharger les données R (dans le répertoire de travail) : colin
- Dans RStudio, installer le package
carà partir de l'installateur ou taper la commande :install.packages("car")
- Exo 1 (Colinéarité détectable par matrice de corrélation)
Considérons le jeu de données pédagogique colinEx. Ce jeu de données de taille 100 décrit quatre variables totalement fictives : une variable à expliquer y et trois régresseurs quantitatifs x1, x2 et x3.
- A partir des traitements préliminaires ci-dessous quels commentaires êtes-vous amenés à faire ?
R> summary(lm(y~x1+x2+x3,data=colinEx)) Call: lm(formula = y ~ x1 + x2 + x3, data = colinEx) Residuals: Min 1Q Median 3Q Max -2.89993 -0.70514 0.06399 0.76046 2.10918 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.7173 0.2640 2.717 0.00782 ** x1 7.7565 9.3562 0.829 0.40915 x2 3.4461 0.3808 9.051 1.63e-14 *** x3 -1.5123 9.3557 -0.162 0.87193 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.027 on 96 degrees of freedom Multiple R-squared: 0.8149, Adjusted R-squared: 0.8091 F-statistic: 140.8 on 3 and 96 DF, p-value: < 2.2e-16
- Un praticien non expérimenté au vu des résultats précédents poursuit son analyse de la manière suivante. Qu'en pensez-vous ?
R> summary(lm(y~x2,data=colinEx)) Call: lm(formula = y ~ x2, data = colinEx) Residuals: Min 1Q Median 3Q Max -4.4023 -1.5064 0.0714 1.5932 4.7542 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.3093 0.4389 7.540 2.39e-11 *** x2 4.1315 0.7646 5.403 4.59e-07 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.073 on 98 degrees of freedom Multiple R-squared: 0.2295, Adjusted R-squared: 0.2217 F-statistic: 29.2 on 1 and 98 DF, p-value: 4.594e-07
Analysez en particulier la chute du coeffcient de détermination.
- Particulièrement surpris par ces résultats, il demande conseil à un de ses collègues qui lui conseille de calculer la matrice de corrélation et d'afficher tous les nuages de points croisant les deux variables.
R> cor(colinEx) y x1 x2 x3 y 1.0000000 0.8104127 0.4790971 0.8094144 x1 0.8104127 1.0000000 0.1032505 0.9992734 x2 0.4790971 0.1032505 1.0000000 0.1028280 x3 0.8094144 0.9992734 0.1028280 1.0000000
Au vu de ces résultats, il s'empresse alors de lancer les deux régressions simples suivantes apparemment rejetées par sa première analyse. Quelle conclusion peut-on en tirer ?
R> summary(lm(y~x1,data=colinEx)) Call: lm(formula = y ~ x1, data = colinEx) Residuals: Min 1Q Median 3Q Max -3.4622 -0.8642 0.0737 0.9347 3.0870 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.3006 0.2652 8.673 9.09e-14 *** x1 6.5803 0.4805 13.694 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.383 on 98 degrees of freedom Multiple R-squared: 0.6568, Adjusted R-squared: 0.6533 F-statistic: 187.5 on 1 and 98 DF, p-value: < 2.2e-16 R> summary(lm(y~x3,data=colinEx)) Call: lm(formula = y ~ x3, data = colinEx) Residuals: Min 1Q Median 3Q Max -3.4386 -0.8432 0.1037 0.9589 3.1305 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.2960 0.2664 8.619 1.19e-13 *** x3 6.5721 0.4817 13.645 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.387 on 98 degrees of freedom Multiple R-squared: 0.6552, Adjusted R-squared: 0.6516 F-statistic: 186.2 on 1 and 98 DF, p-value: < 2.2e-16
Son collègue lui rappelle alors une règle d'or : il est dangereux dans une sélection de modèle pas à pas (descendante) de retirer plus d'un régresseur. Il applique alors cette règle en repartant de sa première analyse et en ne retirant que le regresseur étant le moins significatif.
R> summary(lm(y~x1+x2,data=colinEx)) Call: lm(formula = y ~ x1 + x2, data = colinEx) Residuals: Min 1Q Median 3Q Max -2.8599 -0.7236 0.0752 0.7499 2.1256 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.7146 0.2622 2.726 0.00762 ** x1 6.2452 0.3567 17.509 < 2e-16 *** x2 3.4467 0.3788 9.098 1.19e-14 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.021 on 97 degrees of freedom Multiple R-squared: 0.8148, Adjusted R-squared: 0.811 F-statistic: 213.4 on 2 and 97 DF, p-value: < 2.2e-16
- Il demande alors à son collègue s'il connaît la raison de tels résultats. Ce dernier lui indique alors qu'une colinéarité forte des régresseurs peut engendrer une très forte variabilité des estimateurs et ainsi une difficulté à rejeter l'hypothèse de significativité de certains paramètres de régression (même ceux très corrélés à la variable à expliquer). A partir de la matrice de corrélation, détecter une forte corrélation entre certains régresseurs et à partir des calculs matriciels ci-dessous (où
A%\*%B,solve(A)ett(A)calcule respectivement le produit matriciel entre A et B, l'inverse et la transposée de la matrice A) mettre en évidence le changement des variabilité des estimateurs.
R> x<-cbind(1,x1,x2,x3) R> solve(t(x)%*%x) x1 x2 x3 0.04413933 -0.026367687 -0.026475822 -0.026311662 x1 -0.02636769 0.056777258 -0.003928439 -0.001642811 x2 -0.02647582 -0.003928439 0.059855360 -0.002860594 x3 -0.02631166 -0.001642811 -0.002860594 0.060521811 R> solve(t(x[,-4])%*%x[,-4]) x1 x2 0.03270042 -0.027081894 -0.027719456 x1 -0.02708189 0.056732665 -0.004006087 x2 -0.02771946 -0.004006087 0.059720153
- Exo 2 (Mise en évidence de phénomène de colinéarité)
L'idée est de considérer un modèle théorique dont les régresseurs possèdent un "certain" niveau de colinéarité entre eux, ceci afin d'appréhender les conséquences que cela peut engendrer sur les comportements des estimateurs des paramètres du modèle de régression.
On se propose d'étudier des modèles de régression linéaire à trois régresseurs satisfaisant les hypothèses classiques. Étant donné un vecteur β, et une taille d'échantillon n, on définit trois vecteurs indépendants, réalisations d'une loi uniforme sur [0, 1], notés x1, x2, x3. Le modèle considéré s'écrit alors :
Y = β0 + β1x1 + β2x2 + β3x3′ + U,
où l'on définit x3′ comme une "quasi"-combinaison linéaire de x1, x2 et x3 :
x3′ = α1x1 + α2x2 + (1 − α1 − α2)x3 + U′.
Le vecteur U′ constitue une petite perturbation de la combinaison linéaire "pure" qui permet que la matrice (1,x1,x2,x3′) soit inversible!
Le vecteur β, la taille d'échantillon n ainsi que l'écart-type σ relatif bruit U sont fixés comme ci-dessous :
β = (1, 2, 3, 4)T, n = 200, σ = .2
On donne quatre vecteurs αA, αB, αC, αD définissant 4 modèles (A, B, C et D) distincts de colinéarité.
αA = (0.05, 0.95, 0), αB = (0, 0, 1), αC = (0.5, 0.5, 0) et αD = (0.95, 0.05, 0).
Pour chacun des quatres modèles, exprimez le niveau de colinéarité entre les régresseurs : absence de colinéarité, forte colinéarité,...
On observe quatre matrices de corrélation M1, M2, M3 et M4 correspondant chacune à un modèle (A,B,C,D), quelles associations peut-on espérer?
R> M1 x1 x2 xPrime3 x1 1.00000000 0.06253862 0.96014670 x2 0.06253862 1.00000000 0.08805359 xPrime3 0.96014670 0.08805359 1.00000000 R> M2 x1 x2 xPrime3 x1 1.00000000 0.06253862 0.7060393 x2 0.06253862 1.00000000 0.6505921 xPrime3 0.70603934 0.65059208 1.0000000 R> M3 x1 x2 xPrime3 x1 1.00000000 0.06253862 -0.10538403 x2 0.06253862 1.00000000 -0.03339283 xPrime3 -0.10538403 -0.03339283 1.00000000 R> M4 x1 x2 xPrime3 x1 1.00000000 0.06253862 0.1256600 x2 0.06253862 1.00000000 0.9539574 xPrime3 0.12566000 0.95395738 1.0000000
Pensez-vous pouvoir à la seule vue des matrices de corrélation pouvoir détecter tous les types de colinéarité ?
Rappelez d'où vient la définition du VIF (Variance Inflation Factor). En analysant le calcul des vif de chaque modèle dans l'analyse, et sachant que le VIF1 (resp. VIF2, VIF3 et VIF4) est calculé avec les régresseurs intervenant dans M1 (resp. M2, M3 et M4), retrouvez les associations faites à la question précédente.
R> VIF1 x1 x2 xPrime3 1.058945 11.582197 11.735832 R> VIF2 x1 x2 xPrime3 4.417289 3.822700 7.657322 R> VIF3 x1 x2 xPrime3 12.989023 1.015794 13.045355 R> VIF4 x1 x2 xPrime3 1.014705 1.005321 1.010833
- L'analyse du vif permet-elle de mieux appréhender la colinéarité entre régresseurs ?
- Exo 3 (Utilisation mondiale d'internet)
La problématique est de savoir quels sont les facteurs influençant l'utilisation mondiale d'internet (via le nombre d'internautes). L'analyse sera basée sur un . Dans un premier temps, on va regarder l'influence de la taille de la population et du nombre d'ordinateurs individuels pour 37 pays. On tente alors une modélisation de type log-linéaire sous la forme
(log(int))i = β0 + β1(log(ord))i + β2(log(pop))i + Ui, i = 1, …, 37.
Rappelons qu'envisager un tel modèle revient à supposer que l'élasticité de ord sur int et de pop sur int sont constantes. Par la suite, on supposera (sans y prêter une quelconque attention) que le bruit U satisfait les hypothèses classiques des modèles linéaires (présentées dans le polycopié de cours).
Analysez les sorties ci-dessous
R> require(car) R> attach(internet)
R> summary(lm(log(int)~log(ord)+log(pop))->reg) Call: lm(formula = log(int) ~ log(ord) + log(pop)) Residuals: Min 1Q Median 3Q Max -0.96836 -0.38059 -0.01449 0.21075 2.02775 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.31267 0.79065 1.660 0.106063 log(ord) 0.66784 0.06644 10.052 1.02e-11 *** log(pop) 0.30136 0.06877 4.382 0.000107 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.628 on 34 degrees of freedom Multiple R-squared: 0.7913, Adjusted R-squared: 0.779 F-statistic: 64.45 on 2 and 34 DF, p-value: 2.708e-12 R> vif(reg) log(ord) log(pop) 1.007644 1.007644 R> 1-1/vif(reg) log(ord) log(pop) 0.007586332 0.007586332
On envisage alors en plus d'indicateurs descriptifs d'intégrer un indicateur économique à savoir le de chaque pays. Au vu de la sortie ci-dessous écrire l'équation du modèle et interprétez les résultats. Que confirme la figure en fin d'énoncé ?
R> summary(lm(log(int)~log(ord)+log(pop)+log(pib))->reg2) Call: lm(formula = log(int) ~ log(ord) + log(pop) + log(pib)) Residuals: Min 1Q Median 3Q Max -0.93074 -0.26083 -0.09216 0.25388 1.05011 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.82328 0.67975 4.153 0.000217 *** log(ord) 0.20389 0.10662 1.912 0.064538 . log(pop) -0.03787 0.08647 -0.438 0.664242 log(pib) 0.85683 0.17286 4.957 2.09e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.4826 on 33 degrees of freedom Multiple R-squared: 0.8804, Adjusted R-squared: 0.8695 F-statistic: 80.94 on 3 and 33 DF, p-value: 2.691e-15 R> vif(reg2) log(ord) log(pop) log(pib) 4.393758 2.697517 6.492686 R> 1-1/vif(reg2) log(ord) log(pop) log(pib) 0.7724044 0.6292887 0.8459805
Quelle règle de conduite a été adoptée pour obtenir la sortie ci-dessous ? Interprétez.
R> summary(lm(log(int)~log(ord)+log(pib))->reg3) Call: lm(formula = log(int) ~ log(ord) + log(pib)) Residuals: Min 1Q Median 3Q Max -0.9242 -0.2619 -0.1007 0.2438 1.0186 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.58132 0.39136 6.596 1.47e-07 *** log(ord) 0.23515 0.07827 3.005 0.00497 ** log(pib) 0.79690 0.10438 7.634 7.15e-09 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.4768 on 34 degrees of freedom Multiple R-squared: 0.8797, Adjusted R-squared: 0.8726 F-statistic: 124.3 on 2 and 34 DF, p-value: 2.327e-16 R> vif(reg3) log(ord) log(pib) 2.425311 2.425311 R> 1-1/vif(reg3) log(ord) log(pib) 0.5876818 0.5876818
- Comment retrouver la p-valeur du test de significativité locale du régresseur (indication : on pourra, pour ceux qui le souhaitent, répondre en fournissant l'instruction permettant de la calculer).
- A l'aide d'une calculatrice (ou par simple calcul mental), peut-on penser au vu des données que β2 < 1 au seuil de 5% (remarquez que n est suffisamment grand pour ) ? Faites un dessin (à main levée) représentant la règle de décision et la p−valeur de ce test.
- (question pour les experts) Sans AUCUN CALCUL, proposez une bonne approximation de la p−valeur du test H1 : β2 < 1.6 (indication : 2 × 0.7969 ≃ 1.6).
R> internet pays int pop ord pib 1 etats-unis 123326.000 278058.881 49896.200 7746 2 japon 63955.200 126771.662 7485.780 4202 3 allemagne 28876.900 83029.536 3914.060 2100 ... 33 chine 28697.200 1280775.530 140.599 996 34 thailande 1567.700 61797.751 66.000 157 35 colombie 634.055 40349.388 52.160 85 36 inde 4748.760 1029991.150 45.420 360 37 philippines 410.127 82841.518 29.460 83
- FAQ (A compléter en fonction des questions posées en cours)
Variables explicatives qualitatives
- Résumé de cours
- Exo 1 (Comparaisons modèles qualitatifs)
Trois praticiens sont désireux d'étudier le salaire (noté Sal) d'un individu en fonction d'un indice sur son niveau d'expérience professionnelle (noté Exp) (compris entre 0 et 1 et créé par de brillants spécialistes). Cette étude se limite à des individus dans un certain secteur d'activité. Une variable IndExp a été introduite pour fabriquer des groupes de niveau d'expérience à partir de la variable Exp :
$$ IndExp=\left\{ \begin{array}{ll} Bas & \mbox{si } 0\leq Exp<\frac 13\\ Moyen & \mbox{si } \frac 13\leq Exp<\frac 23\\ Haut & \mbox{si } \frac 23\leq Exp\leq1 \end{array}\right. $$Enfin, ils disposent aussi de la variable Sex (1=Homme et 0=Femme). Pour se divertir, ils décident que chacun d'entre eux propose leur propre traitement à partir d'un même jeu de données :
- la taille d'échantillon est de n=300 individus
- il y a autant (i.e. 50) d'individus de l'échantillon dans chacune des six catégories possibles en croisant les deux variables qualitatives Sex et IndExp.
R> attach(dfCovMod) R> require(xtable)
Traitement du premier praticien : Appréciant les traitements simples, il tente une régression simple de Sal en fonction de Exp dont le résumé est fourni par la commande
Rsuivante :R> summary(lm(Sal~Exp)) Call: lm(formula = Sal ~ Exp) Residuals: Min 1Q Median 3Q Max -859.44 -282.47 9.84 297.94 821.64 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 866.44 42.05 20.61 <2e-16 *** Exp 1815.91 71.99 25.22 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 366.3 on 298 degrees of freedom Multiple R-squared: 0.681, Adjusted R-squared: 0.68 F-statistic: 636.3 on 1 and 298 DF, p-value: < 2.2e-16
Traitement du deuxième praticien : Ce praticien plus expérimenté connaît mieux les modèles de régression. Il décide de traiter le modèle ci-dessous faisant intervenir à la fois la variable a priori qualitative Sex (pouvant être considéré comme une variable quantitative) et l'indice Exp d'expérience professionnelle :
Sali = β0 + β1Expi + β2Sexi + β3(Expi × Sexi)+UiR> summary(lm(Sal~Exp*Sex)) Call: lm(formula = Sal ~ Exp * Sex) Residuals: Min 1Q Median 3Q Max -478.06 -142.38 -9.41 143.13 595.07 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 756.96 32.35 23.400 < 2e-16 *** Exp 1448.66 57.48 25.201 < 2e-16 *** Sex 294.45 46.98 6.267 1.29e-09 *** Exp:Sex 575.75 80.46 7.156 6.57e-12 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 204.1 on 296 degrees of freedom Multiple R-squared: 0.9016, Adjusted R-squared: 0.9007 F-statistic: 904.6 on 3 and 296 DF, p-value: < 2.2e-16
Comparer le coefficient de détermination R2. Pour les deux modèles, quelle(s) valeur(s) prédiriez-vous pour les salaires d'une femme et d'un homme ayant un indice d'expérience professionnelle égal à 0.5 ?
Traitement du troisième praticien : Spécialisé dans les modèles ANOVA (moins dans les modèles de régression), il se propose d'expliquer le Salaire (Sal) en fonction des facteurs (variables qualitatives) Sex et IndExp. L'instruction
R(avec sa sortie standard) conduisant à une telle analyse est donnée ci-dessous:R> summary(aov(Sal~IndExp*Sex)) Df Sum Sq Mean Sq F value Pr(>F) IndExp 2 74368397 37184199 493.40 < 2e-16 *** Sex 1 26370087 26370087 349.91 < 2e-16 *** IndExp:Sex 2 2463488 1231744 16.34 1.86e-07 *** Residuals 294 22156811 75363 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Afin de comparer ses résultats avec ceux de ses collègues, ce praticien (malgré sa moins bonne connaissance des modèles de régression) sait toutefois qu'un modèle ANOVA peut s'écrire comme un modèle de régression linéaire et propose l'analyse suivante :
R> summary(lm(Sal~IndExp*Sex)) Call: lm(formula = Sal ~ IndExp * Sex) Residuals: Min 1Q Median 3Q Max -643.05 -193.87 -3.37 177.69 667.47 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1006.97 37.36 26.955 < 2e-16 *** IndExpMoyen 490.07 52.59 9.318 < 2e-16 *** IndExpHaut 965.24 56.11 17.203 < 2e-16 *** Sex 348.07 55.08 6.319 9.72e-10 *** IndExpMoyen:Sex 309.93 76.89 4.031 7.08e-05 *** IndExpHaut:Sex 436.40 78.97 5.526 7.21e-08 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 274.5 on 294 degrees of freedom Multiple R-squared: 0.8233, Adjusted R-squared: 0.8202 F-statistic: 273.9 on 5 and 294 DF, p-value: < 2.2e-16
A partir de la dernière sortie, écrire l'équation du modèle ( en , correspond à l'indicatrice associée à l'événement IndExp = Moyen).
Quelle(s) valeur(s) prédiriez-vous pour les salaires d'une femme et d'un homme ayant un indice d'expérience professionnelle égal à 0.5 ?
Conclusions : Les trois praticiens confrontent enfin leurs résultats.
Quel(s) modèle(s) vous semble(nt) être le(s) plus intéressant(s) pour le but que se sont fixés les trois praticiens ? (Justifier votre réponse)
Pour comparer les résultats, ils proposent de représenter sur un même graphique les différents modèles ajustés ainsi que le nuage des individus (Triangle=Homme et Croix=Femme) :
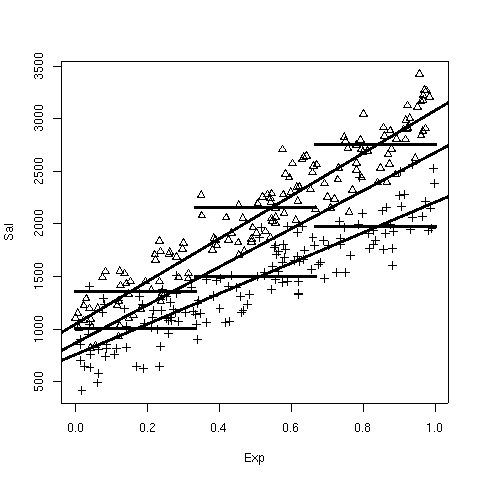
Identifier sur le graphique les droites et segments de droites représentant les trois modèles proposés par ces praticiens.
- Exo2 (Salaire population active en fonction d'indicateurs)
Un praticien se propose d'expliquer le salaire d'une certaine catégorie de la population active en fonction du niveau d'étude et de l'expérience professionnelle. Il s'appuie pour cette analyse sur un jeu de données recueilli auprès de n = 200 individus constitué du salaire mensuel (variable
Sal), d'un indicateur du niveau d'études (variableIndEtu) et d'un indicateur de l'expérience professionnelle (variableIndExp). Ces deux indicateurs ont été calculés par un expert de sorte qu'ils varient entre 0 et 1.On envisage un modèle linéaire standard
Sali = β0 + β1IndEtui + β2IndExpi + Ui
Analysez les résultats de la régression présentés dans le tableau ci-après.R> attach(salaire)
R> summary(lm(Sal~IndEtu+IndExp)) Call: lm(formula = Sal ~ IndEtu + IndExp) Residuals: Min 1Q Median 3Q Max -539.07 -265.83 1.85 273.36 644.93 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 928.93 55.56 16.720 < 2e-16 *** IndEtu 238.91 71.25 3.353 0.000959 *** IndExp 1489.23 73.94 20.140 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 309.8 on 197 degrees of freedom Multiple R-squared: 0.6787, Adjusted R-squared: 0.6755 F-statistic: 208.1 on 2 and 197 DF, p-value: < 2.2e-16
N'ayant pas les moyens d'observer le nuage de points, le praticien sait qu'un bon réflexe est d'observer la répartition des résidus (premier histogramme en haut du graphique ci-après). Que remarquez-vous?
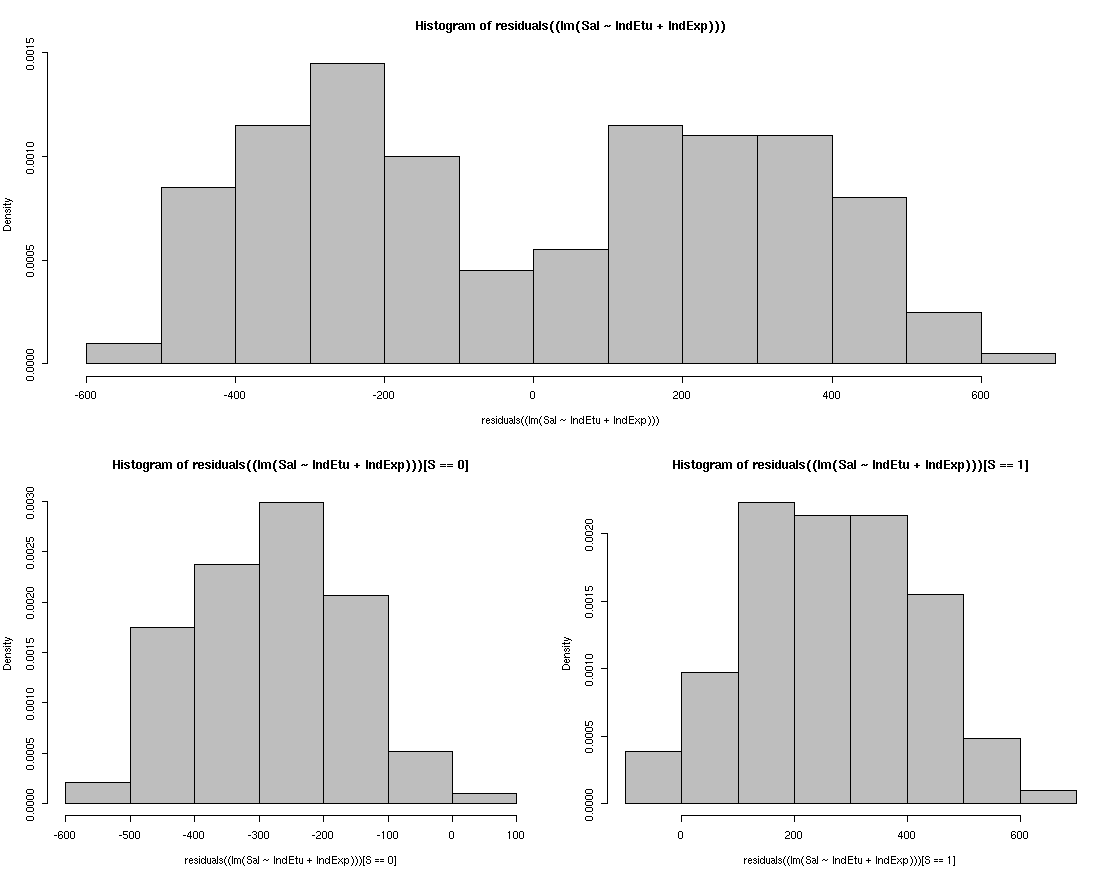
Le praticien décide alors d'introduire une variable binaire S (égale à 1 ou 0) permettant ainsi de classer les individus en deux catégories. Après avoir récolté les informations supplémentaires relatives à S, il ``plot'' les deux autres histogrammes ci-dessus représentant les répartitions des résidus par catégorie. Pourriez-vous expliquer l'analyse du praticien? Et compte tenu de la problématique, quel vous semble être la nature de cette variable discriminante S?
Fort de cette interprétation graphique, le praticien décide d'intégrer S dans le modèle. Cependant, il manque d'expérience dans le traitement de ce type de problème. Lorsqu'il y a deux régresseurs quantitatifs, il sait que la méthode MCO consiste à déterminer dans l'espace de représentation porté par les trois variables le plan le plus proche (``verticalement'') du nuage de points. En revanche, il ne visualise pas très bien ce que fera la méthode après introduction de la variable S. Dans cet espace de représentation (avec les trois mêmes variables), pourriez-vous lui expliquer comment s'interprète la méthode MCO?
Après s'être informé, le praticien envisage alors deux nouveaux modèles :
- Modèle A : on ajoute S au modèle initial.
- Modèle B: on ajoute S × IndEtu (noté
S:IndEtuenR) et S × IndExp (notéS:IndExpenR) au modèle A.
Exprimez géométriquement (via les caractéristiques des plans associés aux deux catégories) la différence entre les deux nouveaux modèles?
Déterminez l'équation de chaque modèle, analysez les résultats de chaque régression et comparez-les avec ceux du modèle initial.
- Modèle A :
R> summary(lm(Sal~IndEtu+IndExp+S)) Call: lm(formula = Sal ~ IndEtu + IndExp + S) Residuals: Min 1Q Median 3Q Max -309.08 -104.64 6.17 101.56 364.73 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 621.74 27.22 22.845 < 2e-16 *** IndEtu 250.43 31.95 7.839 2.83e-13 *** IndExp 1525.13 33.17 45.976 < 2e-16 *** S 550.78 19.67 28.005 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 138.9 on 196 degrees of freedom Multiple R-squared: 0.9358, Adjusted R-squared: 0.9348 F-statistic: 951.7 on 3 and 196 DF, p-value: < 2.2e-16
- Modèle B :
R> summary(lm(Sal~S+IndEtu+IndExp+S:IndEtu+S:IndExp)) Call: lm(formula = Sal ~ S + IndEtu + IndExp + S:IndEtu + S:IndExp) Residuals: Min 1Q Median 3Q Max -225.057 -77.273 -2.623 72.424 261.169 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 819.70 27.73 29.562 < 2e-16 *** S 155.63 38.53 4.039 7.73e-05 *** IndEtu 108.22 36.53 2.963 0.00343 ** IndExp 1275.40 35.25 36.178 < 2e-16 *** S:IndEtu 265.97 49.48 5.375 2.18e-07 *** S:IndExp 530.59 51.25 10.354 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 107.1 on 194 degrees of freedom Multiple R-squared: 0.9622, Adjusted R-squared: 0.9612 F-statistic: 987 on 5 and 194 DF, p-value: < 2.2e-16
- FAQ (A compléter en fonction des questions posées en cours)
Intervalle de confiance et Prédiction
- Intervalle de confiance à 1 − α (généralement $=5%) de niveau de confiance
- Objectif : déterminer, à partir d'un futur jeu de données $(\mathbf{Y}|\underline{\mathbf{x}})$ représentable par un futur nuage de points, une future estimation $\widehat{\beta_j}(\mathbf{Y}|\underline{\mathbf{x}})$ de βj.
- Via l'A.E.P.
- cela consiste à imaginer réaliser un très grand nombre (voire même une infinité) m de nuage de points ainsi que les intervalles de confiance $IC_{\beta_j}(\mathbf{y}_{[k]}|\underline{\mathbf{x}})$ associés
- et on sait qu'approximativement 95% (si α = 5%) de ces intervalles de confiance contiennent le vrai paramètre inconnnu βj
- En conclusion, l'unique intervalle de confiance $IC_{\beta_j}(\mathbf{y}|\underline{\mathbf{x}})$ est l'un parmi une infinité d'intervalles de confiance dont on sait qu'approximativement 95% (si α = 5%) contiendraient le vrai paramètre inconnnu βj.
Intervalle de prévision (A compléter)
FAQ (A compléter en fonction des questions posées en cours)
Les supports de cours
Cours et TDs
Complément
- Un document de Cours pdf qui, néanmoins, n'est pas le support de cours officiel du cours d'Introduction à l'Econométrie donné en L3.
Data
- cinema.RData : cinema
- dataLM.RData : canada, champ, chomage, ecofict, initie, maison, voiture
- colin.RData : colinEx
- internet.RData : internet
- dfCovMod.RData : dfCovMod
- salaire.RData : salaire
Anciens examens
Attention : pas au format QCM mais contenus similaires au futur Examen sous forme de QCM
- Examen 2004/2005 avec correction
- Examen 2005/2006 avec correction